| Constructing Functions from a Table:
| | Constructing functions from a table of values may be a very simple procedure, or it may be a more challenging process, depending upon the data provided in the table. Before we kickoff, we should check to meet if the table Tin BE represented past an exponential role . Call up that exponential functions grow by mutual factors over equal intervals. Are the x-values changing past the aforementioned increment, and do successive y-values have the aforementioned ratio or common gene? (You may see the term "multiplier" used to represent "common factor".) | Example 1:
The table at the correct shows values from an exponential function of the grade
f (x) = abx . Find the values of a and b, and limited an equation that may be represented by this table. This example would be labeled Piece of cake since the y-intercept is given at (0,7) and the ordered pairs increment by the same x increase of one. | 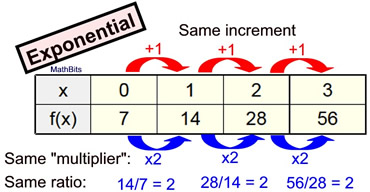 | Solution:
In the last lesson, we saw that the y-intercept of f (10) = ab10 is (0, a) . So, in this instance, we tin can see that the y-intercept is at (0,7) making a = seven. ANS: a = 7 | Since nosotros have already noted that the common factor ("multiplier") is two in this tabular array, we know the value for b is ii. ANS: b = 2
Equation: f (x) = 7•(2) x | What happens when the x-increment is NOT +ane ? Case 2:
The table at the correct shows values from an exponential function. Detect the values of a and b, and express an equation that may be represented by this table. Notice that the "same increment" is now +5 (instead of +1). This will affect the final reply, making this problem's difficulty level HARD. | 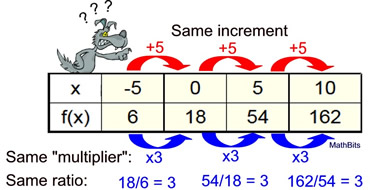 | Solution:
Nosotros will proceed with the assumption that our reply will be of the form f (x) = abten .
Again, we know that the y -intercept of f (x) = abx is (0, a) . So, in this example, we tin see that the y-intercept is at (0,18) making a = 18. ANS: a = 18 | The common factor (or "multiplier") is iii in this table, so the b value is 3.
ANS: b = 3
Equation: f (x) = 18•(3) x |  | This is not the correct equation!
f (5) = eighteen•(3)5 = 4374 ≠ 54
|
And so, what went incorrect? The problem is that our formula, f (x) = ab10 , assumes that the increase on x will exist +one. And so, when it sees +5 to the right of 0, it assumes that information technology is the fifth increment to the right of zero, and not the first increase to the right of zippo. The common cistron is then applied five times, instead of only once, and we get an answer of 4374 instead of 54. | 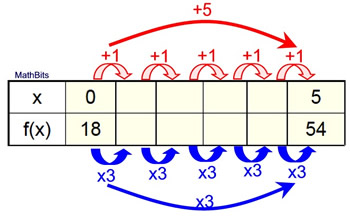 | | How can nosotros "ready" this problem? Nosotros need our formula to understand that an increment of +5 is the first location to the right of nil. The formula is making the increase 5 times larger than it needs to be. Since x represents the increments, we demand to divide ten by 5 to obtain an accurate equation. | Equation: f (10) = 18•(three) 10/ 5
Our original formula needs to be amended for this new situation. → |  | where c = the
x-increase value | | | Is at that place an easier way to bargain with increments non equal to +one ? Example 2 AGAIN:
The table at the right shows values from an exponential function. Detect the values of a and b, and express an equation that may be represented by this table. With use of the graphing calculator, the difficulty level will be lowered to MODERATE. |  | Solution: We will be using the graphing computer's ability to fix an exponential regression equation to discover the solution to this problem. Under these conditions, nosotros volition be obtaining the actual equation (and not an approximation, or best fit, for the equation).
Notation r two = i and r = 1 telling united states we hit ALL of the points for an bodily equation.
| Enter the four points into
L1 and L2 nether STAT
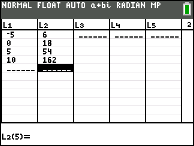 | From STAT → CALC
cull 0:ExpReg
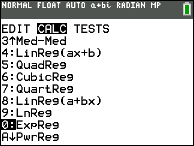 | Use the lists where you stored the points. Make full in Y1 for the graph.
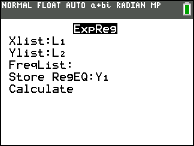 | | 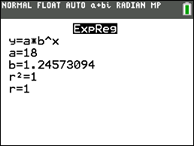 | a = 18 and b = ane.24573094
Equation: f (x) = xviii•(1.24573094) x
But this doesn't lucifer our previous answer, or does it?
Put those exponent skills to utilise!

It does lucifer! | | What practice nosotros practise when no consistent 10-increment is given ? Example 3:
The table at the correct shows values from an exponential function of the form
f (x) = abx . Find the values of a and b, and limited an equation that may be represented by this table. This example would be labeled MODERATE difficulty, | Find: No abiding increment on 10.
No constant multiplier on f (x).
Now, what do we do? | 10 | -i | 1 | 4 | vi | nine | | f(x) | 0.75 | three | 24 | 96 | 768 | We DO KNOW that this is an exponential function since the question says it is an exponential role. | Solution:
Nosotros need a new plan of attack on this problem since information technology is not immediately obvious what the common factor ("multiplier") may be. Choose ii of the points that are closest to 1 another, such as x = -1 and ten = 1, or 10 = 4 and x = half dozen. If the decimal bothers yous, choose x = iv and ten = 6. Create a new section of the table filling in the missing increments between the two points yous chose. | 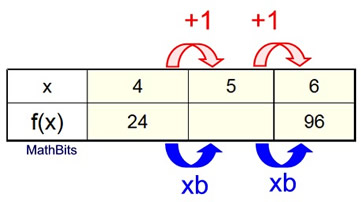 | | You can see that we represented the "multiplier" between each of the increments with "x b". Now, algebraically, to get from f (x) = 24 to f (x) = 96 we have: 24 • b • b = 96 → 24b two = 96 →b 2 = 4 → b = 2
Nosotros now have: f (x) = a • two x
To get a, substitute ane of the points, such as (4,24).
24 = a • 24 = a • 16 → a = 24/xvi = 1.5 Equation: f (10) = 1.5•(ii) ten |  Amalgam Functions from TWO Input-Output PAIRS: | | | "Practise two points always determine an exponential function?"
Bold that we are speaking about an exponential role of the form f (x) = ab10 , the answer is "Yep, under certain weather." The atmospheric condition are that (1) a ≠ 0 (because you would have a direct line), (2) that the x-coordinates not be the same (you wouldn't have a part) and (3) that the y-coordinates of the points be not-aught with the aforementioned signs (call up the asymptotic nature of the graphs of these exponential functions - always all above, or all beneath, the 10-axis). So, how practice we change ii points into an exponential part?
Constructing functions given only 2 input-output pairs (or ordered pairs) tin can be accomplished in a variety of ways. The choice of solution method volition depend upon the nature of the given pairs. For example, if you are given the y-intercept every bit i pair, the solution will exist fast and easy. If, on the other paw, you are given two generic pairs, perhaps containing decimals, yous volition demand to practice more work to discover the solution. Allow's take a look at some of the possibilities. | | Instance 1: (easy) Discover an exponential function of the class f(x) = ab10 given the facts that f(0) = 12 and f(5) = 2916. | | Solution:
f (0) = 12 → (0,12)
f (5) = 2916 → (5, 2916) | Find a: The y-intercept is 12, then a = 12.
We now have f (10) = 12•bten | Find b: Substitute:
2916 = 12•b v
243 = b 5
b = 3 | | Equation: f (x) = 12•(3) x (you can Check this answer by plugging in the two points.) | | Example iii: (harder) Find an exponential function of the class f(x) = abx which will pass through the points (one,30) and (3,187.5). | | This problem will also require a organisation of equations. But, this time, we volition be using an emptying method to solve, instead of the substitution method shown in Example 2. | | Solution:
Substitute the points into the formula:
(1, thirty) → f (ane) = ab 1 = 30
(3,187.5) → f (three) = ab 3 = 187.v | Divide the two equations:
This will be easier if yous start with the larger exponent on top. 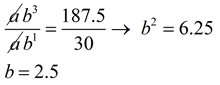
| Plug in to find a :
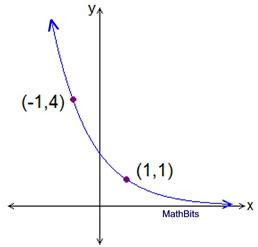
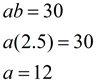 | | Equation: f (x) = 12•(2.5) x (you can Cheque this respond past plugging in the two points.) | | Example four: (harder yet) Find an exponential function of the form f(ten) = abx which will pass through the points (-three,256) and (two, ¼). Round to nearest hundredths if needed. | | Again, this solution will utilize a system of equations with an elimination method. | | Solution:
Substitute the points into the formula:
(-3, 256) → f (-three) = ab -3 = 256
(ii,¼) → f (2) = ab ii = ¼  Remember non to round until y'all reach the final answer. The slightest modify in b can affect the answer. If non "asked" to round, leave the full calculator entry. Remember non to round until y'all reach the final answer. The slightest modify in b can affect the answer. If non "asked" to round, leave the full calculator entry. | Divide the two equations:
This volition be easier if you lot showtime with the larger exponent on tiptop. 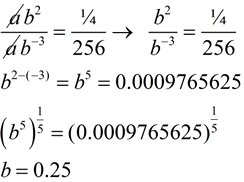
| Plug in to find a :
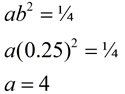 | | Equation: f (x) = iv•(0.25) ten | Case four AGAIN: (easier) Find an exponential part of the form f(10) = abx which will pass through the points (-3,256) and (two, ¼). Round to nearest hundredths if needed.
Nosotros volition solve this once again, using the exponential regression capabilities of the graphing calculator. | | Solution:
Enter the ii points into L1 and L2 under STAT
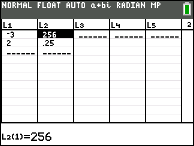 | From STAT → CALC choose 0:ExpReg 
| Exist sure your lists match where you stored the points. Fill up in Y1 if y'all want to see the graph.
 | | 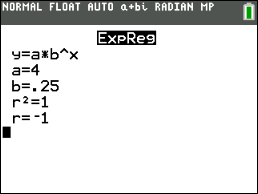 | a = iv
b = .25 Equation: f (x) = four•(0.25) x Aren't calculators wonderful!!
|  NOTE: The re-posting of materials (in office or whole) from this site to the Net is copyright violation
and is not considered "fair utilize" for educators. Please read the "Terms of Use". | |





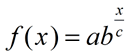






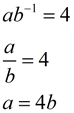
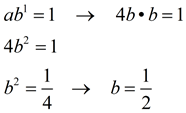
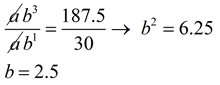
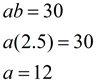
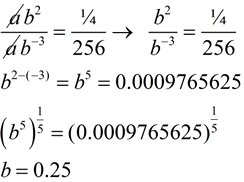
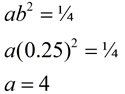



0 Response to "Writing Exponential Functions From Tables"
Post a Comment