How To Find Determinant 2x2
2-past-2 Determinants
A determinant is based on a square matrix, but the determinant is done upwardly in absolute-value confined instead of square brackets. In that location is a lot that you can do with (and learn from) determinants, merely you'll probable need to wait for an advanced course to learn about them. In this lesson, I'll but show y'all how to compute 2×2 and 3×iii determinants. (It is possible to compute larger determinants, but the procedure is much more complicated, then I won't carp with that here.)
Content Continues Below
Given a matrix named " B ", the determinant of B is denoted by "det(B)", pronounced equally "the determinant of B ", or just "det-bee".
A determinant tin can be derived just from a foursquare matrix. (Some people have tried to ascertain diverse pseudo-determinants for non-foursquare matrices, only I don't think they're catching on. All you'll ever hear of volition be determinants for square matrices. Because reasons.) If your matrix isn't square, it doesn't have a determinant.
How do yous get a determinant from a matrix?
If you take a foursquare matrix, its determinant is written past taking the aforementioned grid of numbers, removing the foursquare brackets "[]", and replacing those brackets with absolute-value bars "||", equally shown below:
If this is
"the matrix A "...
...then this is "the determinant of A "
(To blazon absolute-value bars, use the "piping" character, which is probably on the same keyboard key every bit the "backslash" graphic symbol.)
Just as absolute values can be evaluated and simplified to go a unmarried number, so can determinants. The process for evaluating determinants is pretty messy, so let's start unproblematic, with the 2×2 example.
How exercise y'all detect the determinant of a 2-by-ii matrix?
For a 2×two matrix, its determinant is institute by subtracting the products of its diagonals, which is a fancy way of proverb in words what the following says in pictures:
the matrix A with variables:
the determinant of A (or "det A "):

the matrix A with numbers:
the determinant of A (or "det A "):

In other words, to take the determinant of a 2×2 matrix, you follow these steps:
- Multiply the values along the top-left to bottom-right diagonal
- Multiply the values forth the bottom-left to top-right diagonal
- Subtract the second product from the showtime
- Simplify to go the value of the 2-past-2 determinant
"But wait!" I hear you weep; "Aren't absolute values always supposed to be positive? The numerical matrix above is shown as having a negative determinant. What's upwardly with that?" You make a proficient betoken.
Can a determinant be negative?
Yes, determinants can be negative! Determinants are similar to absolute values, and apply the same notation, but they are not identical, and one of the differences is that determinants tin indeed be negative.
What is an example of finding a 2-by-2 determinant?
- Evaluate the following determinant:
In this exercise, they've given me a determinant (rather than a matrix), and so I tin can get correct to work. I multiply the diagonals (highlighted with regal arrows in my working below), and subtract:
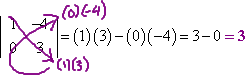
Then my answer is:
det(A) = 3
- Find the determinant of the following matrix:
Here, they've given me a matrix, and asked me to find the determinant of it.
First, I'll convert from a matrix to a determinant by swapping out the brackets for absolute-value bars. So I'll multiply along the diagonals (blueish arrows beneath), subtract the products, and simplify to get my numerical answer:
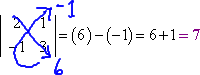
Then my answer is:
det(A) = 7
That'south really all there is to two-past-2 determinants. Merely make sure you multiply and subtract in the right order, and you'll be fine.
How To Find Determinant 2x2,
Source: https://www.purplemath.com/modules/determs.htm
Posted by: reynoldsfoure1965.blogspot.com


0 Response to "How To Find Determinant 2x2"
Post a Comment